27 × 38 inch poster


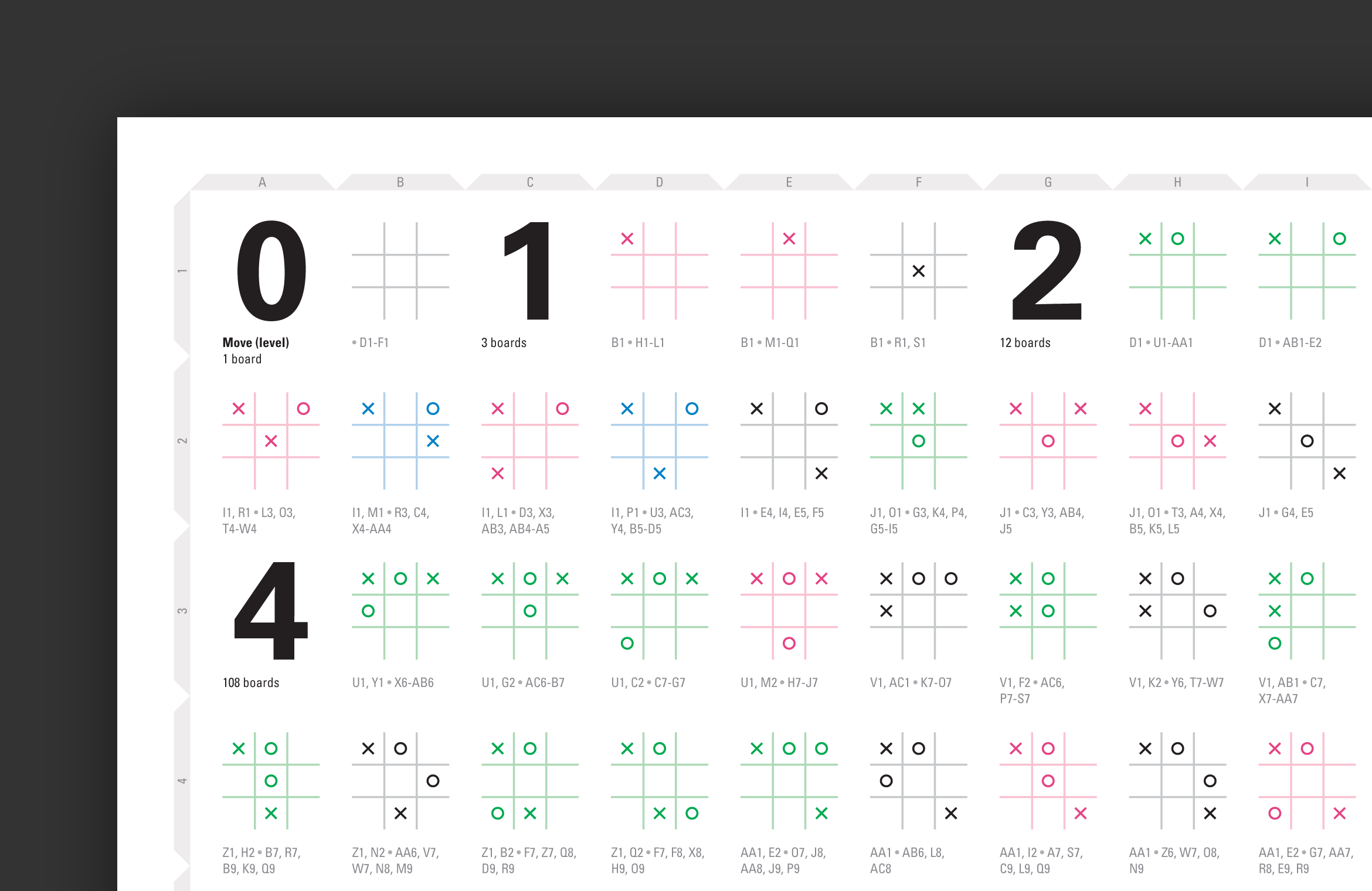
Each board configuration list of boards that precede and succeed it.
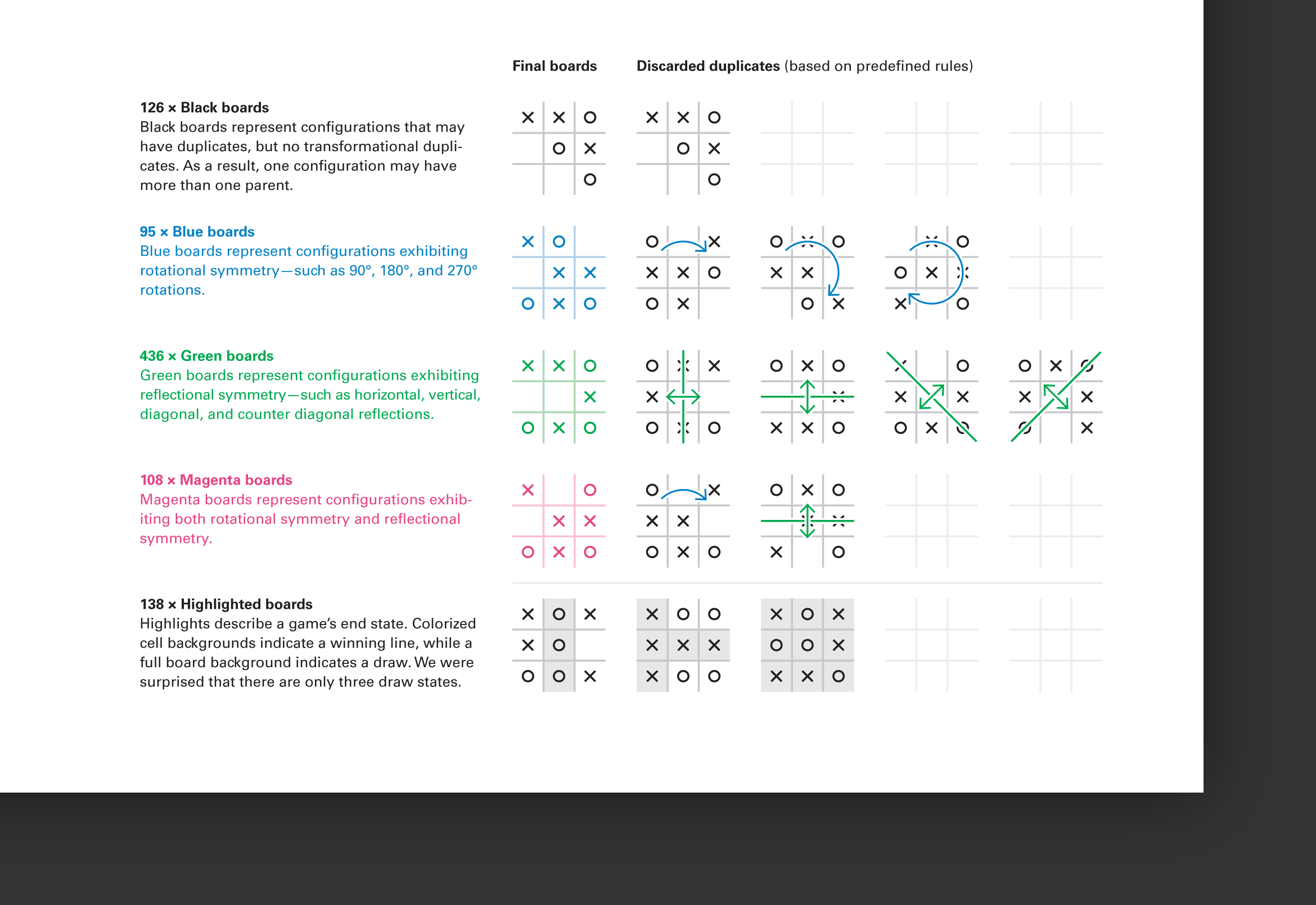
Excluding rotational and reflectional symmetries to reduce the solution space
The interactive website places emphasis on the connections between boards.





In this visualization, we examine what Herbert Simon might call the “solution space” for tic-tac-toe, a compound visualization of all its solutions—every legal game move and the connections between them—in a single artifact.
How large is the solution space? Well, for the first move, there are 9 cells available. For the second, there are 8, and so on. Follow to completion, and we get 9×8×7×6×5×4×3×2×1 or 9! boards for the final level. For each level n of gameplay, there are 9!/(9-n)! boards in total. By adding the level totals together, we get an “upper bound” of 986,410 boards—far too many to represent meaningfully.
For the visualization to be meaningful, the number of boards must be reduced. We do this by introducing 3 rules; (1) removing duplicate boards reduces the count to 6,046, (2) removing illegal moves (play after a win) reduces the count to 5,478, and (3) by removing symmetric duplicates (rotational and reflectional) we are left with 765 unique boards. This poster displays them all in a matrix.
Information Design
Computational Design
Solution Space
2019








